Hi,
I couldn’t find any results on performance benchmark so I thought I might ask it here. Please excuse me if it is already published somewhere that I just didn’t manage to find.
Is there some high level results of comparing Optizelle to other solves such as IPOPT for large scale problems? (assuming same linear solver, etc…)
cheers,
Yunlong
Well, the short answer is no.
The longer answer is more complicated. Basically, Optizelle was designed to be extensible, but it doesn’t include everything necessary to benchmark appropriately against something like IPOPT without a lot of work that we felt was directed elsewhere. Specifically, if a problem contains equality constraints or nonlinear inequality constraints, then we require a fast linear system solver to obtain good performance. This is due to the augmented system solves that affect things like the nullspace projection, quasi-normal step, and multiplier solves. Theoretically, this is not required, but practically it is because GMRES performs poorly without a preconditioner and the linear system solvers and factorizations are a good way to get a perfect preconditioner. Anyway, once we start to factorize a system, there are a number of cascading consequences. It requires us to handle dense and sparse systems, so we typically double the number of factorizations that we need to handle. Then, of course, we need to have a sane interface to generate these systems. Should these generation come from automatic differentiation? Should they come from a manual interface? How do we support both? Of course, we could just have a bare bones interface and then depend on something like AMPL to generate the systems, but most of our paying work involves problems that are not well suited to AMPL. Specifically for benchmarking, it makes sense to have an interface to CUTEst, but this requires labor to put together and their interface for solvers is different than what Optizelle supports by default. Their Hessian is pre-combined whereas the one for Optizelle comes in pieces and this causes some issues.
All of this is certainly resolvable and largely has been dealt with, but in a code that has yet to be released. That new code has taken far, far too long to get released and I really do apologize for that. Certainly, things like a year of pandemic haven’t helped, but it really is close to being done. We do in fact have benchmarks with the appropriate interfaces for others to verify our results once everything is released.
So, to recap. No external benchmark comparisons. Getting them required a rethink in the design and a complete rewrite of the code. There is a soon-to-be-released code that does have them. Please stay tuned for that one.
Thanks for your detailed reply Joe, really appreciate it!
I’d be lying if I say I understand all the intricate details that you were kindly explaining 
but I think I get the gist… Maybe I can explain a little bit about my thoughts from a user’s perspective.
What led me to Optizelle?
As you mentioned: it is extensible I have an NLP with both nonlinear equality and inequality, for which the Jacobian has certain structure that can be exploited. I’m sure the standard linear solvers already deals with sparsity quite nicely, but I wonder if I could gain further speed improvement by exploiting the structure manually. This is something not so easy to achieve with solvers such as IPOPT, which pretty much has everything ‘baked in’ (except for a choice of dynamically linking to a linear solver dll)
What was I asking myself before testing the water?
I hope this kind of user story is useful. I’ll keep an eye on your website/forum for the new release. And lastly, I cannot imagine how much effort it takes to keep such an open source project afloat, thank you very much for that.
That project sounds very cool and thanks for sharing!
And, yes, a lot of the nuance as to how things will perform will come down to the linear solver. With respect to IPOPT vs Optizelle, one of the core differences is what linear system gets solved. As a disclaimer, I do not work on the IPOPT code, so there may be some errors in what I’m about to write. Wächter and Biegler describe their algorithm in the paper On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. The linear system that they solve can be seen in equation 13:
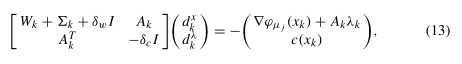
To solve that system, they hook into a variety of HSL routines, which are helpfully described by HSL themselves here.
Now, there are a number of differences and similarities between Optizelle and IPOPT. The general framework for getting the inequalities into the Hessian is similar. Using their notation, the W + Sigma in the above equation is mostly the same. However, Optizelle does not solve the larger system above. Instead, it really comes down to solving, in the above notation, A'*A. Technically, we’re solving a larger augmented system, but it really comes down to that linear algebra solve. Now, the nice thing about that solve rather than the larger system that IPOPT uses is that we get to be more creative on how solve that system. For example, if A represents a PDE, we can then precondition the linear system with a piece of code that does a PDE solve using something like a Runge-Kutta method rather than use a factorization.
That said, it’s not quite as simple as just solving this other system. In order to get to this smaller system to solve, we solve what’s called an augmented system, which is a linear system of the form
[I A]
[A' 0]
To get to this system, we have to employ what is called a composite step SQP method, which breaks apart the step into one that moves toward feasiblity and one that moves toward optimality. This has its own set of difficulties, but it means that the steps that Optizelle and IPOPT take are fundamentally different. And, to be clear, there are lots of other differences from globalization to barrier parameters, but these are the larger differences with respect to linear solvers, which you’ve mentioned. As a brief aside, NITRO also uses a composite step method, but it handles the inequalities and their reduction somewhat differently.
OK, outside of this general academic curiosity, how does the the robustness compare? With no inequalities, it’s probably a wash. With inequalities, IPOPT is probably more robust. This is something that I’m sensitive to and have largely resolved in the new algorithm. There’s a number of reasons as to why. Candidly, the IPOPT algorithm is good and their team has done a fantastic job of refining the algorithm. Depending on the kind of problem, Optizelle has some trouble with repeating running itself into the boundary. That took me some time to understand why and, with the new algorithm, I don’t worry about it ever. At some point in time, I hope to write a good comparison article on why this happens and how it was resolved.
Hopefully that helps a bit and I hope I’m not being too coy. Thanks for the feedback. That helps, really. I’ll try to answer any other questions as best I can.
thanks for the detailed explanation which gave me a lot of useful insights!
It sounds like I should simply wait for the new release Do you know roughly when it might come and if it is going to stay on the same license?
Not a problem.
As far as the new version, it should be this year. How late sort of depends on a number of factors. Generally speaking, we have some client work lined up over the next few months, which tends to slow, but not stop, the product development. My personal hope is sometime over the summer. It’s a little tricky because it’s not just the code, but the documentation as well as the scientific papers, but it should all come together.
As far as license, I’ve gone back and forth on things. At the moment, my inclination is to move to something like the MPL license, which shouldn’t restrict closed source commercial usage, but makes it clear that algorithmic improvements to the library should be shared. Some of this is to also make it clear to clients that their products are theirs, but our libraries, which are used in their products, need to remain open. This is always worked out contractually as well, but sometimes it helps for the license to align with this principle. That said, it is somewhat more restrictive than the current BSD license. I’ve soured a little on the BSD license due to the ambiguity with respect to patents, but, to be clear, I’m not a lawyer. Since you’ve asked about it, are there any particular concerns that you have?
Hello, I happened to open this thread.
In fact, I have been working on numerical optimal control recently, and in order to speed up the solution of NLP, I have finally come up with the same idea as you: Is it possible to incorporate some known information into the underlying solution process, but since snopt is not open source and I am not familiar with IPOPT, this idea has been shelved for the time being, but seeing your ideas today makes me really want to ask: have you made any new progress recently?
If so, please let me know.
Hi, cporoske! Sorry for seeing this message so late; I’ve been on travel and I missed a few notifications. That said, I don’t really have too much to report as of now. I’ve been tied up with client work the last few months and I don’t have a direct funding source for the new optimization codes. Ostensibly, that’s not a problem and I will have them done and open sourced, but it does mean that it becomes a lower priority at times when I have work that actually pays. Certainly, if anyone has access to grant money, I’ll be more than happy to task everything back to the open source code development. However, short of that, it’s been painfully slow.
All that said, I’m actually coming out of work crunch, so I’ve some internal goals set for June for the optimizer. I hope to have a better idea of where everything is at after that.
Thanks for checking in! I’ll keep working at it.